Die SARS-COV-2 Pandemie beeinflusst bereits seit Monaten unser Leben. Die Wirksamkeit von Maßnahmen gegen die Pandemie kann anhand epidemiologischer Modelle überprüft und vorausgesagt werden. Die Corona SEIR Workbench verwendet hierfür ein SEIR Model und kombiniert eine graphische Ausgabe der Ergebnisse mit einer einfachen Parametereingabe. Die modellierten Daten können länderweise mit den SARS-COV-2 Infektionsdaten der Johns-Hopkins-Universität verglichen werden. Für Deutschland können zusätzlich die R₀-Werte des Robert-Koch-Instituts angezeigt werden.
Aktueller Stand der COVID-19-Pandemie
Seit Dezember 2019 hält der Corona Virus SARS-COV-2 und seine COVID-19 Erkrankung die Welt mit einer Pandemie in Atem. Dabei war das Auftreten einer vergleichbaren Pandemie nur eine Frage der Zeit. Schätzungen gehen von einem Auftreten vergleichbarer Pandemien alle 20-30 Jahre aus1.
Da stand heute noch kein Impfstoff flächendeckend zur Verfügung steht, werden viele verschiedene, nicht-medizinische Maßnahmen zur Eindämmung der Pandemie eingesetzt. Diese reichen von Alltagsmasken über Abstände zwischen Personen, Schließung von öffentlichen Einrichtungen, Sportstätten und der Gastronomie bis zu Kontaktbeschränkungen alle mit dem Ziel, die Virus-Ausbreitung zu reduzieren. Teststrategien und Kontaktnachverfolgung sollen infizierte Personen möglichst schnell erkennen und dann in einer Quarantäne isolieren. Alle diese Maßnahmen sollen das Infektionsgeschehen kontrollieren und trotzdem möglichst wenig Einschränkungen für die Bevölkerung und wenig negative wirtschaftliche Folgen haben.
Voraussetzung für die Kontrolle der Pandemie ist eine möglichst gute Datenbasis. Diese wird in Deutschland vom Robert Koch-Institut über die Gesundheitsämter in ermittelt. International trägt das Center for Systems Science and Engineering (CSSE) der Johns-Hopkins-Universität SARS-COV-2 Infektionszahlen zusammen und stellt diese zur Verfügung.
Das zentrale Ziel der Pandemie-Kontrolle ist es, die Überlastung des Gesundheitssystems zu vermeiden, damit alle an COVID 19 Erkrankten eine möglichst optimale medizinische Versorgung bekommen. Darüber hinaus ist eine möglichst geringe Infektionsrate wünschenswert, um die gesundheitlichen Folgen auf die Bevölkerung zu minimieren.
Auf der Basis der ermittelten Daten können Epidemie-Modelle Voraussagen über das Infektionsgeschehen für die Zukunft treffen. Infektionszahlen entwickeln sich exponentiell. Daher können die Zuwachszahlen an Erkrankten schnell aus dem Ruder laufen und das Gesundheitssystem überlasten. Aus diesem Grund sind ein frühes Einschreiten und eine Überprüfung der getroffenen Maßnahmen essentiell für eine Kontrolle der Pandemie.
Das SEIR Modell
Das SEIR-Modell gehört zur Klasse der Kompartiment-Modelle, die Personen in Kompartimente einsortiert. Das SEIR-Modell teilt die Bevölkerung in die vier Kompartimente „Susceptible“ (anfällige Personen), „Exposed“ (exponierte Personen), „Infectious“ (infektiöse Personen) und „Recovered“ (erholte bzw. gestorbene Personen) ein:
Bei der Modellierung wandern Personen von einem Kompartiment ins nächste. Die Berechnung findet je Zeiteinheit statt. Als Zeiteinheit wird meist ein Tag verwendet.
Am Anfang einer Epidemie sind so gut wie alle Personen gesund und im Kompartiment „Susceptible“. Alle Personen in diesem Kompartiment können mit dem Corona-Virus infiziert werden. Nach einer Infektion wandert eine Person in das Kompartiment „Exposed“ und verbleibt dort für die mittlere Inkubationsdauer der Erkrankung. Zu dieser Zeit ist die Person noch nicht für andere Personen ansteckend. Eine Studie2 im Januar hat die mittlere Inkubationszeit mit 5,2 Tagen angegeben. Eine ausführliche Diskussion ist bei Byrne et al.3 zu finden.
Sobald die kranke Person Viren verteilt und andere Personen infizieren kann, kommt Sie aus dem Kompartiment „Exposed“ in das Kompartiment „Infectious“. In diesem „Topf“ befinden sich die Personen, die die Pandemie antreiben. Die kranke Person bleibt in diesem Kompartiment für die mittlere Infektionszeit von 2,9 Tagen4.
Die mittlere Infektionszeit ist nicht mit der maximalen Infektionsdauer zu verwechseln, die bei der Quarantäne einer kranken Person eine Rolle spielt und bis zu 14 Tage lang sein kann. Die mittlere Infektionsdauer wird auch durch die Diagnostik beeinflusst, da eine kranke Person häufig bei Symptombeginn getestet und dann isoliert wird.
Nachdem eine Person die Krankheit überstanden hat und nicht mehr infektiös ist, wandert diese aus dem Kompartiment „Infectious“ in das Kompartiment „Recovered“. Sie ist zu diesem Zeitpunkt immun gegen eine erneute Ansteckung mit SARS-COV-2. Neben der Erholung kann die Person ebenso an COVID 19 versterben. Das SEIR Modell trifft hier keine Unterscheidung und sortiert die Person in beiden Fällen in das Kompartiment „Recovered“.
Die Mathematik hinter dem SEIR Modell
In der Modellierung des SEIR Modells wird die Veränderung aller vier Kompartimente je Zeiteinheit berechnet. Im ersten Schritt werden ΔS anfällige Personen im Kompartiment S durch infektiöse Personen im Kompartiment I infiziert. Hierfür neben der Menge der infektiösen Personen die Basisreproduktionszahl R0 ausschlaggebend:
Für SARS-COV-2 wurde ein R0-Wert von 3,45 für eine ungebremste Verbreitung ermittelt. Das heißt im Mittel steckt ein Infizierter 3,4 weitere anfällige Personen an. Ein R0-Wert größer 1 sorgt für ein exponentielles Wachstum von Infektionen, während ein R0-Wert kleiner 1 zu einer abnehmende Zahl von neu infizierten Personen sorgt.
Die Änderung der infektiösen Personen ΔE ergibt sich aus der Inkubationsdauer:
Daher wächst die Zahl der infektiösen Personen mit einem gewissen Zeitverzug nach ihrer Infektion.
Nachdem die Krankheit überstanden ist oder die infektiöse Person isoliert wurde, wandert diese in das Kompartiment R. Die Anzahl ΔI ergibt sich aus der mittleren Infektiositätsdauer:
Die verwendeten Symbole in den Gleichungen stehen für folgende Werte:
Die neuen Personenanzahlen S‘, E‘, I‘ und R‘ in den einzelnen Kompartimenten S, E, I und R nach einer Zeiteinheit können nach folgenden Formeln berechnet werden:
Die Workbench
Das Ziel der Corona Workbench war es eine Infrastruktur für die Modellierung einer Epidemie zu schaffen. Dazu gehört neben der Modellierung auch die graphische Darstellung der Ergebnisse je Zeiteinheit und die leichte Änderung von Modellierungsparametern. Um die Modellierung mit historischen Daten zu vergleichen sollten Bevölkerungsgrößen, Infektionszahlen und R0-Werte parallel angezeigt werden können. Darüber hinaus sollte die Software leicht erweiterbar sein, um auch andere Modelle schnell zu realisieren.
Architektur der Workbench
Wir haben uns bei der Corona SEIR Workbench für einen klassenbasierten Ansatz mit C# entscheiden, da sich die einzelnen Komponenten so deutlich besser isolieren und warten lassen. Darüber hinaus bietet .Net eine sehr gute Performance und C# verfügt über alle Möglichkeiten einer Hochsprache mit objektorientierten und funktionalen Sprachelementen. Mittels Linq können hier einfach Mengenoperationen eingebaut werden.
Für eine graphische Anzeige verwenden wir die Microsoft Windows Forms Charting Bibliothek6, die mit Visual Studio kommt. Für die Benutzeroberfläche verwenden wir XAML aus der Windows Presentation Foundation und kombinieren beides in einem .Net Core 3.1 Projekt.
Um die Daten möglichst vieler Länder darzustellen, benutzen wir die Infektionszahlen des CSSE der Johns-Hopkins-Universität, die von Datopian täglich nach Ländern aggregiert werden. Für historische R0-Werte verwenden wir die vom Robert Koch-Institut täglich veröffentlichten Nowcasting-Werte . Bevölkerungszahlen ermitteln wir aus dem API der World Bank. Alle Daten werden nur einmal täglich aus dem Web geladen und dann temporär für weitere Modellierungen gespeichert.
Einen auf Python basierten Ansatz der SEIR Modellierung von Corona hat Pina Merkert7 im Heise c‘t Magazin vorgestellt. Der Python Code ist ebenfalls auf Github zu finden ist.
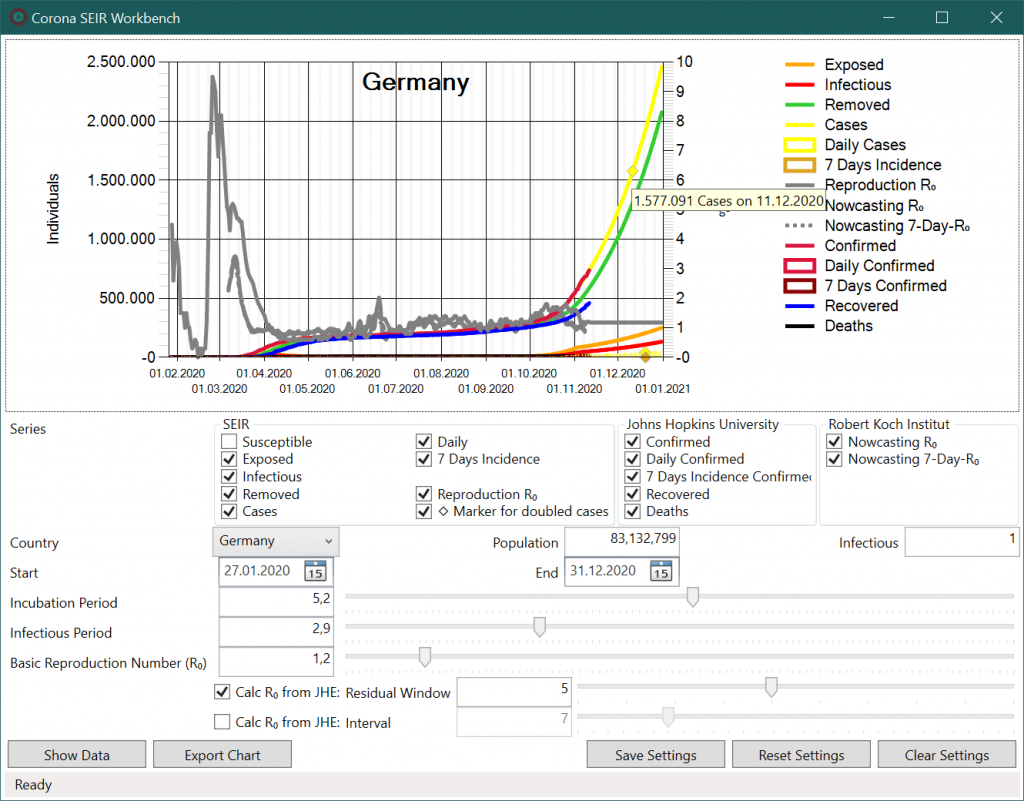
Die Benutzeroberfläche der Workbench
Die Benutzeroberfläche sollte möglichst einfach sein und mit Visual Studio leicht von C# Programmierern erweitert werden können. Das Hauptfenster gliedert sich in drei Blöcke:
Im oberen Bereich wird ein Diagramm angezeigt. Alle Werte werden je Datum auf der horizontalen Achse dargestellt. Die linke, vertikale Achse bezieht sich auf Fallzahlen während die rechte Achse R0-Werte anzeigt. Tägliche Inzidenzwerte werden als Balken in der Graphik und Kästchen in der Legende ausgegeben. Zusätzlich wird für modellierte Gesamt-Fallzahlen, Tages-Fallzahlen und mittlere 7-Tages Fallzahlen eine Raute für den Wert angezeigt, an dem sich die Zahlen des aktuellen Tages verdoppelt haben. Im Tooltip wird der Wert unter dem Mauszeiger für das dargestellte Datum angezeigt.
Unterhalb des Diagramms können einzelne Kurven in dem Bereich „Series“ aus- und eingeblendet werden. Die Skalierung der Achsen erfolgt automatisch, so dass es meist Sinn macht, die Kurve der anfälligen Personen („Susceptible“) mit ihrem großen Werten auszublenden.
Die nächsten Parameter bestimmen das Land und den Modellierungszeitraum. Darunter können SEIR-Parameter für die mittlere Inkubationszeit, den mittleren Infektionszeitraum und die Basisreproduktionszahl R0 eingestellt werden. Änderungen werden sofort übernommen, die Modellierung neu berechnet und die Ergebnisse im Diagramm dargestellt.
Neben einem konstanten R0-Wert kann dieser auf der Basis der historischen Fallzahlen berechnet werden. Die Grundlage für die Berechnung des R0-Wertes liefert eine „Solver“ Komponente, die das SEIR nach der Levenberg-Marquardt-Methode8 löst. Im ersten Lösungsverfahren wird für jeden einzelnen Tag im SEIR Modell in einem zukünftigen Fenster von n-Tagen der R0-Wert mit dem geringsten Fehler in den Fallzahlen berechnet. Je größer das Fenster ist, desto stärker wird die Kurve geglättet. Beim zweiten Verfahren wird der R0-Wert mit der geringsten Abweichung in den Fallzahlen für ein bestimmtes Intervall berechnet. Beide „Solver“-Komponenten verwenden immer den größten R0-Werte, der den kleinsten Fehler liefert, wenn die Fehler mehrerer R0-Werte identisch sind.
Zum Schluss wird er Mittelwert des R0-Wertes aus den letzten 5 Tagen ermittelt und dann für alle zukünftigen Zeiteinheiten verwendet. Dieser zukünftige Mittelwert kann manuell angepasst werden, um Maßnahmen des Infektionsschutzes im Modell zu berücksichtigen.
Im unteren Teil des Hauptfensters werden alle Funktionen der Workbench als Schaltflächen angezeigt. „Show Data“ zeigt alle im Diagramm dargestellten Werte als Tabelle an. Von hier können die Werte über die Zwischenablage in andere Programme, wie z.B. Mcirosoft Excel übernommen werden. Mittels „Export Chart“ kann das Diagramm als Graphik in verschiedenen Formaten oder auch als CSV-Datei exportiert werden.
Einstellungen des Diagramms und des SEIR Modells können mit der Schaltfläche „Save Settings“ gespeichert werden. Die gespeicherten Einstellungen werden automatisch beim Start der Anwendung geladen. Mit „Reset Settings“ werden diese auf die Standardeinstellungen zurückgesetzt. Die Schaltfläche „Clear Settings“ setzt wie „Reset Settings“ alle Einstellungen zurück, blendet jedoch alle Kurven im Diagramm aus. Diese Funktion ist für die Erstellung eigener Diagramme bequemer, da sonst viele Kurven erst ausgeblendet werden müssten.
Ergebnisse der Workbench
Die einfachste Modellierung verwendet ein SEIR-Modell mit einer ungebremsten Ausbreitung des SARS-COV-2 Virus und einer konstanten Basisreproduktionszahl von 3,4 für Deutschland.
In diesem Fall hätte sich fast die gesamte Bevölkerung im April und Mai diesen Jahres infiziert. Die tatsächlichen Fallzahlen der Johns-Hopkins-Universität für Deutschland zeigen jedoch einen anderen Verlauf:
Der Grund für den unterschiedlichen Verlauf erklärt sich aus den R0-Werten des Robert Koch-Instituts, die im April von 3,4 auf unter 1 gefallen sind:
Die Basisreproduktionszahl hat sich durch den deutschlandweiten Lockdown und Kontaktverbote deutlich reduziert. Der Peek Mitte Juni entstand wahrscheinlich durch die hohe Anzahl an Corona-Infizierten im Kreis Gütersloh verursacht durch Fleischereibetriebe. Da es sich um einen lokalen Ausbruch handelte, konnte dieser recht schnell eingedämmt werden.
Wenn die historischen R0-Werte nach der Levenberg-Marquardt-Methode8 berechnet werden, zeigt das SEIR-Modell die gleichen Werte. Die Fallzahlen (gelbe Linie) entsprechen den tatsächlichen Infektionszahlen (rote Linie) bis zum 13.11.2020, dem aktuellen Datum. Wenn der aktuelle R0-Wert in Höhe von 1,2 beibehalten wird, ist für die Zukunft jedoch ein weiterer starker Anstieg zu befürchten und eine Verdoppelung der Fallzahlen findet in weniger als einem Monat statt (gelbe Raute).
Der berechnete R0-Werte im März ist deutlich höher als der vom RKI ermittelte Wert. Dies liegt an den geringen Fallzahlen im Februar und Anfang März. Es ist eine grundsätzliche Schwäche des R0-Wertes, bei geringen Fallzahlen hohe Schwankungen aufzuweisen. Daher wurde auch im Sommer auf die 7-Tage Inzidenzzahl als Beurteilungskriterium umgestellt.
Auch hier entspricht die Kurve der Johns-Hopkins-Daten dem SEIR Modell. Hier wurde jedoch für die Zukunft ein R0-Wert von 0.9 verwendet, der nahe bei dem 7-Tages R0-Wert vom 8.11.2020 des RKI aus der Nowcasting-Tabelle vom 13.11.2020 liegt. In diesem Fall würde die 7-Tages Inzidenz Anfang Dezember unter 100 Fälle pro Tag fallen.
Die unterschiedlichen Szenarien zeigen, wie kritisch die Basisreproduktionszahl für die Weiterentwicklung der Pandemie ist. Ein R0-Wert über 1 ist der Treiber der Epidemie.
Das Klassenmodell der Workbench
Die Corona Workbench arbeitet mit einem Interface-basierten Klassenmodell für die Berechnung von SEIR-Modellen. Jedes SEIR-Modell verfügt über eine ISEIR-Schnittstelle, in der die SEIR-Parameter angegeben werden und die Personenanzahl für die Kompartimente S, E, I und R abgefragt werden können. Mit einer Calc-Methode werden diese für eine bestimmte Anzahl von Zeiteinheiten berechnet. Die Berechnung der Kompartimente S‘, E‘, I‘ und R‘ in der Calc-Methode erfolgt über statische Funktionen und kann hier einfach angepasst werden. Die Initialisierung der ISEIR-Modelle findet über Konstruktoren statt.
Um ein ISEIR-Objekt anzuzeigen wird dieses an eine Sicht übergeben. Dies kann entweder eine ISeriesView für diskrete Zeitabschnitte oder eine IDateSeriesView für ein Zeitintervall mit Start- und Enddatum sein. Über die CalcAsync-Methoden wird das Modell berechnet und die einzelnen Datenpunkte in Datenserien gespeichert. Die Sicht SEIRR0DateSeriesView erlaubt die Übergabe verschiedener R0-Werte für ein Datum.
Die Berechnung der R0-Werte erfolgt über Solver mit einer IR0Solver-Schnittstelle. Diese implementiert eine Solve-Methode, die eine Sequenz von R0-Werten zurückgibt. Das Interface wird von einer SEIRR0Solver-Klasse implementiert, die für jeden Tag die Fallzahlen eines SEIR-Modells mit den tatsächlichen Fallzahlen vergleicht und den besten R0-Wert für den Tag mit der Levenberg-Marquardt-Methode8 berechnet. Dafür werden der Einfachheit halber aller R0-Werte zwischen 0 und 10 in 0,1 Schritten berechnet und der Wert mit der kleinsten Abweichung in den Fallzahlen zurückgegeben.
Historische Infektionszahlen des Center for Systems Science and Engineering der Johns-Hopkins werden über ein JHU-Objekt ermittelt und als Datenserien über die Sicht JHUDateSeiriesView zurückgegeben. Da es sich bei den Daten der Johns-Hopkins-Universität um einen Spezialfall handelt, wurde kein Interface für die JHU-Klasse verwendet:
Das JHU-Objekt speichert die abgerufenen Daten in einer temporären CSV-Datei zwischen und versucht diese möglichst schnell zu parsen.
Den gleichen Ansatz verfolgt die RKINowcasting-Klasse, die die Nowcasting-Excel-Liste des Robert Koch-Instituts einmal täglich herunterlädt und die Spalten „Punktschätzer der Reproduktionszahl R“, sowie „Punktschätzer des 7-Tage-R Wertes“ für ein Datum zurückgibt.
Die aktuelle Bevölkerungszahl eines Landes wird mit der Klasse WPPopulation über das World-Bank API ermittelt.
Ausblick
Die Corona SEIR Workbench liefert eine einfache Infrastruktur zur Modellierung von Epidemien. Sie verwendet Standardkomponenten, wie das Windows Forms Charting für die Anzeige von Diagrammen und die Windows Presentation Foundation für die Benutzeroberfläche. Aktuelle epidemiologische Daten für COVID 19 können komponentenweise aus dem Web geladen werden und mit Modellwerten verglichen werden.
Dadurch kann die Anwendung mit wenig Aufwand erweitert werden. Erweiterungen wären z.B. eine zusätzliche Datenbasis mit den Infektionsdaten des RKI und einer regionalen Aufteilung für Deutschland. Darüber hinaus könnten zukünftige R0-Werte nicht nur als einzelne Konstante, sondern als Funktion oder Wertetabelle angegeben werden.
Die Berechnung des R0-Wertes ist maßgeblich von der Testsituation abhängig. So verfälscht eine hohe Dunkelziffer von Infizierten die Berechnung des R0-Wertes aus historischen Infektionszahlen. Da besonders junge Infizierte asymptomatisch sein können, ist die Altersverteilung der Infizierten bei der Abschätzung der Dunkelziffer relevant. Darüber hinaus existieren Rückkopplungsschleifen mit Epidemie-Maßnahmen, wie z.B. bei der Quarantäne von Reiserückkehrern aus Risikogebieten die wahrscheinlich häufiger trotz Symptomen ohne Testung von infizierten Personen unterlaufen wurde.
Vorschau in neuem Tab(öffnet in neuem Tab)
Eine interessante Erweiterung des SEIR-Modells wäre die Berücksichtigung von Superspreading-Ereignissen und Perkolation, die sich durch die Überdispersion von Corona-Infektionen ergibt. Zur Nachverfolgung von Superspreading-Ereignissen bietet sich ein Cluster-Tagebuch an.
Für die Berechnung des Aufwandes einer medizinischen Versorgung ist die Aufteilung der infizierten Personen in leichte Fälle und schwere Fälle notwendig. Hierfür sind jedoch Daten zur Altersstruktur der Infizierten notwendig.
Eine viel weitergehende Modellierung wären z.B. die Ansätze von Frau Prof. Priesemann zur altersabhängige Todesrate von Infizierten (infection fatality rate, IFR)9 oder die Auswirkungen einer Test-, Nachverfolgungs- und Isolierungsstrategie (TTI, Test-Trace-Isolate)10.
Letztendlich ist die Corona SEIR Workbench nur eine Infrastruktur und wartet auf den nächsten Einsatz. Wir sind gespannt, welche Einsatzmöglichkeiten Sie finden.
Downloads
| Corona SEIR Workbench 1.0.1 | 2,98 MB | Corona SEIR Workbench Version 1.0.1 Programm, erfordert .NET Core 3.1 Runtime |
Aktuelle Version:
| Corona SEIR Workbench 2.3.0 | 2 MB | Corona SEIR Workbench Version 2.3.0 Programm, erfordert .NET Core 5.0 Runtime |
| Corona SEIR Workbench 2.3.0 Setup | 119 MB | Corona SEIR Workbench Version 2.3.0 Setup mit Runtime |
Weitere Informationen
- Corona SEIR Workbench Quellcode auf Github
- Bekämpfung von Superspreading während der COVID-19-Pandemie
- Download .NET Core 3.1 Runtime
- Softwareentwicklung
- .Net mit C#
- English version of this post
1. Interview mit Gunther Kraut, Handelsblatt vom 02.05.2020.↩
2. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, Ren R, Leung KSM, Lau EHY, Wong JY, Xing X, Xiang N, Wu Y, Li C, Chen Q, Li D, Liu T, Zhao J, Liu M, Tu W, Chen C, Jin L, Yang R, Wang Q, Zhou S, Wang R, Liu H, Luo Y, Liu Y, Shao G, Li H, Tao Z, Yang Y, Deng Z, Liu B, Ma Z, Zhang Y, Shi G, Lam TTY, Wu JT, Gao GF, Cowling BJ, Yang B, Leung GM, Feng Z. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020 Mar 26;382(13):1199-1207. doi: 10.1056/NEJMoa2001316. Epub 2020 Jan 29. PMID: 31995857; PMCID: PMC7121484.↩
3. Byrne AW, McEvoy D, Collins AB, et al., Inferred duration of infectious period of SARS-CoV-2: rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases, BMJ Open 2020;10:e039856. doi:10.1136/bmjopen-2020-039856 .↩
4. Wu, Jianhong & Leung, Kathy & Leung, Gabriel. (2020). Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. The Lancet. 395. 10.1016/S0140-6736(20)30260-9..↩
5. Wu, Joseph T et al., Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study, The Lancet, 2020 Volume 395, Issue 10225, 689 – 697.↩
6. Beispiele unter https://github.com/dotnet/winforms-datavisualization/tree/main/sample.↩
7. Pina Merkert, ODE an Corona – Covid-19-Vorhersagen mit dem SEIR Modell, c’t 2020, Heft 11, Seite 124-127↩
8. Craig Markwardt, Least Squares Fi-ng and Equaton Solving with MPFIT, University of Maryland and NASA’s Goddard Spaceflight Center, http://purl.com/net/mpfit 2009‐04-15 .↩
9. Linden, Matthias, u. a. „The foreshadow of a second wave: An analysis of current COVID-19 fatalities in Germany“. arXiv:2010.05850 [physics, q-bio], Oktober 2020. arXiv.org, http://arxiv.org/abs/2010.05850..↩
10. Contreras, Sebastian, u. a. „The challenges of containing SARS-CoV-2 via test-trace-and-isolate“. arXiv:2009.05732 [q-bio], November 2020. arXiv.org, http://arxiv.org/abs/2009.05732..↩